1. 概述

Dijkstra算法是由计算机科学家Edsger W. Dijkstra在1956年提出的，用来寻找图形中节点之间的最短路径。从图中的某个顶点出发到达另外一个顶点的所经过的边的权重和最小的一条路径，称为最短路径。

它的主要特点是以起始点为中心向外层层扩展(广度优先搜索思想)，直到扩展到终点为止。如下图所示，扩展和访问下一个节点最主要考虑累计成本$g(n)$的大小。

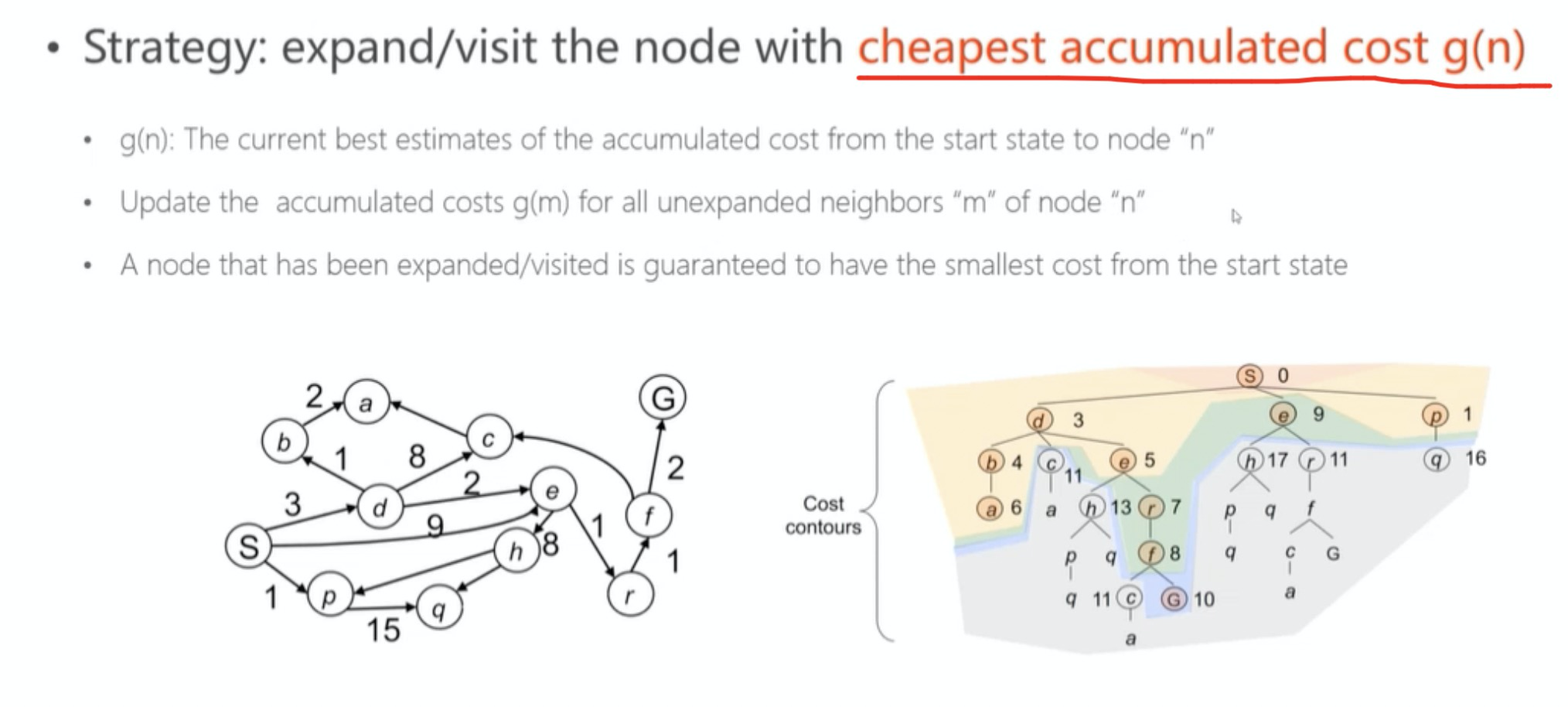
核心思想：设G=(V,E)是一个带权有向图，把图中顶点集合V分成两组，第一组为已求出最短路径的顶点集合（用S表示，初始时S中只有一个源点，以后每求得一条最短路径 , 就将加入到集合S中，直到全部顶点都加入到S中，算法就结束了），第二组为其余未确定最短路径的顶点集合（用U表示），按最短路径长度的递增次序依次把第二组的顶点加入S中。在加入的过程中，总保持从源点v到S中各顶点的最短路径长度不大于从源点v到U中任何顶点的最短路径长度。此外，每个顶点对应一个距离，S中的顶点的距离就是从v到此顶点的最短路径长度，U中的顶点的距离，是从v到此顶点只包括S中的顶点为中间顶点的当前最短路径长度。

2. 算法详解

给定一个有权图，如下图所示：

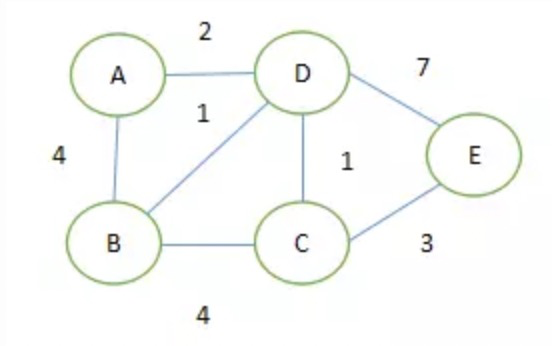
（1）指定一个节点，例如我们要计算 ‘A’ 到其他节点的最短路径。

（2）引入两个集合（S、U），S集合包含已求出的最短路径的点（以及相应的最短长度），U集合包含未求出最短路径的点（以及A到该点的路径，如上图所示，A->C由于没有直接相连初始时为∞）。

（3）初始化两个集合，S集合初始时，只有当前要计算的节点，A->A = 0，U集合初始时为 A->B = 4, A->C = ∞, A->D = 2, A->E = ∞。直接连接的定义长度，其他认为不可达。

（4）从U集合中找出路径最短的点，加入S集合，例如 A->D = 2。

（5）更新U集合路径，如果D到B,C,E的距离与AD距离之和小于A到B,C,E的距离，则更新U。

（6）循环执行（4）和（5）两步骤，直至遍历结束，得到A到其他节点的最短路径。

3. 代码实现

给定如下有向加权图：

graph_list = [
    [0, 30, 15, M, M, M],
    [5, 0, M, M, 20, 30],
    [M, 10, 0, M, M, 15],
    [M, M, M, 0, M, M],
    [M, M, M, 10, 0, M],
    [M, M, M, 30, 10, 0]
]

任意节点到其余节点的最短路径实现代码如下：

import numpy as np
from collections import defaultdict
from heapq import *


def dijkstra(graph_dict, from_node, to_node):
    Shortest_path, cost = [], -1
    q, seen = [(0, from_node, ())], set()
    while q:
        (cost, v1, path) = heappop(q)
        if v1 not in seen:
            seen.add(v1)
            path = (v1, path)
            if v1 == to_node:
                break
            for v2, c in graph_dict.get(v1, ()):
                if v2 not in seen:
                    heappush(q, (cost + c, v2, path))

    if v1 != to_node:
        cost = -1
        Shortest_path = []
        return cost, Shortest_path
    else:
        left = path[0]
        Shortest_path.append(left)
        right = path[1]
        while len(right) > 0:
            left = right[0]
            Shortest_path.append(left)
            right = right[1]
        Shortest_path.reverse()

    return cost, Shortest_path


def dijkstra_all(graph_dict):
    Shortest_path_dict = defaultdict(dict)
    for i in nodes:
        for j in nodes:
            if i != j:
                cost, Shortest_path = dijkstra(graph_dict, i, j)
                Shortest_path_dict[i][j] = Shortest_path

    return Shortest_path_dict


if __name__ == '__main__':
    nodes = ['s1', 's2', 's3', 's4', 's5', 's6']
    M = float("inf")
    graph_list = [
        [0, 30, 15, M, M, M],
        [5, 0, M, M, 20, 30],
        [M, 10, 0, M, M, 15],
        [M, M, M, 0, M, M],
        [M, M, M, 10, 0, M],
        [M, M, M, 30, 10, 0]
    ]

    graph_edges = []
    for i in nodes:
        for j in nodes:
            if i != j and graph_list[nodes.index(i)][nodes.index(j)] != M:
                graph_edges.append((i, j, graph_list[nodes.index(i)][nodes.index(j)]))

    graph_dict = defaultdict(list)
    for tail, head, cost in graph_edges:
        graph_dict[tail].append((head, cost))

    Shortest_path_dict = dijkstra_all(graph_dict)
    for key in Shortest_path_dict:
        print("'%s': %s," % (key, Shortest_path_dict[key]))

输出结果如下所示：

Shortest_path_dict = {
's1': {'s2': ['s1', 's3', 's2'], 's3': ['s1', 's3'], 's4': ['s1', 's3', 's6', 's5', 's4'], 's5': ['s1', 's3', 's6', 's5'], 's6': ['s1', 's3', 's6']},
's2': {'s1': ['s2', 's1'], 's3': ['s2', 's1', 's3'], 's4': ['s2', 's5', 's4'], 's5': ['s2', 's5'], 's6': ['s2', 's6']},
's3': {'s1': ['s3', 's2', 's1'], 's2': ['s3', 's2'], 's4': ['s3', 's6', 's5', 's4'], 's5': ['s3', 's6', 's5'], 's6': ['s3', 's6']},
's4': {'s1': [], 's2': [], 's3': [], 's5': [], 's6': []},
's5': {'s1': [], 's2': [], 's3': [], 's4': ['s5', 's4'], 's6': []},
's6': {'s1': [], 's2': [], 's3': [], 's4': ['s6', 's5', 's4'], 's5': ['s6', 's5']},
}

4. 总结和讨论

优点
- 完备的：只要有解，就能够找到解
- 最优的：找到的解是最优的
局限性
- 计算复杂度高：求解的过程中，是按照均匀的向外扩散的，类似于穷举搜索，类似于BFS

算法对比

序号	算法	主要思想	优缺点
1	BFS	按照宽度向外扩展节点	可以找到最优解，但计算复杂度高
2	DFS	按照深度向外扩展节点	可以找到最优解，计算复杂度高
3	GBFS	按照宽度以一定朝向扩展节点	计算复杂度相对较低，但可能无法找到最优解
4	Dijkstra	按照一定宽度以一定成本函数值向外扩展节点	完备的且最优的，但计算复杂度较高

路径规划（三）-Dijkstra算法

1. 概述

2. 算法详解

3. 代码实现

4. 总结和讨论

5. 参考